Question

Suppose we have M pegs $(p_1,p_2,\cdots,p_M)$ and all N disks are on $p_1$. We need to move them to $p_M$ under the Lucas rule. How many moves are required at least?

Basic solution

The Frame-Stewart Algorithm’s pipeline is as followed:

  1. Move $T$ disks from $p_i$ to $p_j$, where $j\neq M$
  2. Move $N-T$ disks from $p_i$ to $p_M$
  3. Move $T$ disks from $p_j$ to $p_M$

This algorithm divides the solution into three stages, which actually divides the Hanoi tower into a main-tower(the lower $N-T$ disks) and a sub-tower(the upper $T$ disks).

image-20220911164413342

For example, the Hanoi tower with 3 disks can be divided into a main-tower in the first peg with only one disk, the sub-tower is in the third peg with two disks. In this way, a Hanoi problem with more disks can be transferred into a solved Hanoi problem with less disks(the sub-tower’s move is a solved problem). When there are more than three pegs, the Hanoi tower can be divided into many sub-towers recursively. Finally, we can get the recursive formula: $Hanoi[M][N]:=\min_{1\leq r<N}(2Hanoi[M][r]+Hanoi[M-1][N-r])$, the initial condition is $Hanoi[3][n]=2^n-1,\ \ Hanoi[n][1]=1$

The proof of the Frame-Stewart Algorithm used in four pegs can be found in A new lower bound for the Towers of Hanoi problem

Thinking of sub-minimum moves

We know the minimum amount of necessary moves to finish a Hanoi task of $Hanoi[3][n]$ is $2^n-1$. But what’s the sub-minimum moves of it?

We can consider it in the same way as the optimal method: Think back from the last step, we must move the sub-tower with upper n - 1 disks to the buffer peg then move the disk at bottom from the start peg to the target peg. Finally, we need to move the sub-tower with upper n - 1 disks to the target peg. The process indicates that the extra move compared with the optimal solution comes from the moving of the sub-tower, which means it’s also a recursive process.

However, there is a limitation that we can’t move the same disk continuously, which means we need to start from $Hanoi[3][2]$ (Define: $Hanoi[n][1]$ doesn’t have a sub-minimum solution). I enumerate all cases where the distribution of disks are the same to find the sub-optimal solution of $Hanoi[3][2]$ as followed.

The optimal solution:

image-20220911184114398

The sub-optimal solution(two moves more than the optimal one):

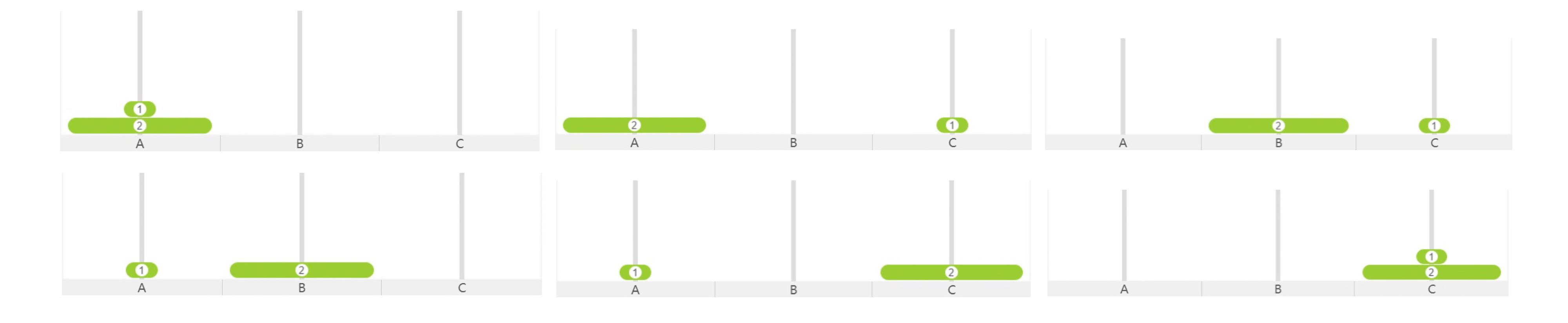
image-20220911184211854

Also, I have verified nine moves in $Hanoi[3][3]$ by hand, which is also two moves more than the optimal solution. It indicates that when there are three pegs, the sub-minimal solution might have two moves more than the optimal solution at the most. Then I get the formula: $subHanoi[3][n]=2^n+1,\ \ where \ \ n\geq2$.

Finally, I guess I can extend the result to the situation where has more pegs, the recursive formula of sub-minimum moves is

Furthermore, I calculate the exact number for $Hanoi[7][23]$ matrix and $subHanoi[7][23]$ with my computer, the source codes in C are in the appendix. The outputs are as followed:

image-20220911174822210

M pegs N disks minimum moves sub-minimum moves
5 13 55 57
7 13 39 41
5 19 103 105
7 19 63 65
5 23 159 161
7 23 87 89

Appendix: Source Code (C)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
#include<stdio.h>
#define M (7)
#define N (23)
#define minof(x,y) (((x)>(y))?(y):(x))
int hanoi[M + 1][N + 1];
int subHanoi[M + 1][N + 1];
//M pegs with N disks
//Hanoi[M][N] := min{2Hanoi[M][r]+Hanoi[M-1][N-r]} when integer r in [1,N)
void hanoiInitialize(){
    int i;
    for(i = 1;i <= N;i++){
        hanoi[3][i] = (1 << i) - 1;
        if(i != 1){
            subHanoi[3][i] = hanoi[3][i] + 2;
        }else{
            subHanoi[3][i] = __INT_MAX__/2;
        }
    }
    for(i = 1;i <= M;i++){
        hanoi[i][1] = 1;
        subHanoi[i][1] = __INT_MAX__/2;
    }
}
void ansPrint(){
    printf("Answer format [M:N]->X,Y\nrefers M pegs with N disks need X moves at least"
    " while the sub-minimum solution is Y\n");
    printf("[7:23]->%d,%d\n",hanoi[7][23],subHanoi[7][23]);
    printf("[5:23]->%d,%d\n",hanoi[5][23],subHanoi[5][23]);
    printf("[7:19]->%d,%d\n",hanoi[7][19],subHanoi[7][19]);
    printf("[5:19]->%d,%d\n",hanoi[5][19],subHanoi[5][19]);
    printf("[7:13]->%d,%d\n",hanoi[7][13],subHanoi[7][13]);
    printf("[5:13]->%d,%d\n",hanoi[5][13],subHanoi[5][13]);
}
void quiryMore(){
    int quitOrNot = 1;
    while(1){
        printf("\nInput two numbers separated by blank as M and N to represent M pegs with N disks(m < 3 or n < 1 to quit)\n"
        "-1 refers no solution\n->INPUT:");
        int m, n;
        scanf("%d%d",&m, &n);
        if(m < 3||n < 1){
            break;
        }
        printf("->OUTPUT:M pegs with N disks need %d moves at least\n->OUTPUT:while the sub-minimum solution is %d\n", hanoi[m][n], subHanoi[m][n]);
    }
}
void renewSubHanoi(){
    int i, j;
    for(i = 1;i <= M;i++){
        for(j = 1;j <= N;j++){
            if(subHanoi[i][j] == __INT_MAX__/2){
                subHanoi[i][j] = -1;
            }
        }
    }
}

int main(){
    hanoiInitialize();
    int i, j;
    for(i = 4;i <= M;i++){
        for(j = 2;j <= N;j++){
            int min = __INT_MAX__, k, subMin = __INT_MAX__;
            for(k = 1;k < j;k++){
                int curMin = 2 * hanoi[i][k] + hanoi[i - 1][j - k];
                int curSubMin = minof(hanoi[i][k] + subHanoi[i][k] + hanoi[i - 1][j - k], 2 * hanoi[i][k] + subHanoi[i - 1][j - k]);
                if(curMin < min){
                    min = curMin;
                }
                if(curSubMin < subMin){
                    subMin = curSubMin;
                }
            }
            hanoi[i][j] = min;
            subHanoi[i][j] = subMin;
        }
    }
    renewSubHanoi();
    ansPrint();
    quiryMore();
    return 0;
}